roofit manual

下载文章
RooFit Manual
ROOTUsersGuide
ROOT: Tutorials

1 安装和设置RooFit

1.1 安装root和roofit

roofit库是标准root发行版的一部分，并且预编译在二进制发行版中，可以通过root.cern.ch获取。如果您从源代码发行版编译 ROOT，则必须在运行 configure 时使用标志 –enable-roofit。你可以在Installing ROOT链接中找到安装适合你系统的方法，推荐Mac用户使用package manager进行安装，例如homebrew，根据介绍安装完之后就可以在终端使用 brew install root自动安装ROOT了。除此之外，还有其他很多应用都能使用brew安装，有点像一个应用商店一样，适合新手使用。

1.2 设置交互式root环境

只要在命令行引用了 RooFit 类之一，ROOT 就会自动加载 RooFit 库 libRooFitCore 和 libRooFit。方便起见，建议你ROOT登录脚本中添加下面的命令using namespace RooFit;，这样你就能在命令行中使用RooFit命名空间中的辅助函数了。这个命令也会自动加载RooFit库。这篇指导的所有例子都是建立在你已经加载RooFit命名空间的基础上的。

using namespace RooFit;

一般情况下你需要将你的程序写入到一个程序文件中，在这个程序开头你需要加入一些头文件和命名空间，这样你在使用root yourprogm.C的时候就能加载RooFit库了

1.3 root使用补充

Root 中的命令都是由.开始的，包括一些linux shell 命令比如像.ls

root[] .?  //this command will list all the Cling commands
root[] .L <filename>  //load [filename]
root[] .x <filename>  //load and execute [filename]
root[] .ls    //用root打开一个文件之后可以用这个命令看里面的文件内容

2 Getting started

按你胃, 先上手做再说！这部分会带你做简单的模型去拟合数据。目的是让你熟悉一些基本概念，并且能快速地做一些有用的事情。在接下来的小节中我们会更仔细地探索RooFit几个方面。

2.1 构建模型

RooFit中一个关键概念是以面向对象的方式构建模型的。每个RooFit的类都有一个对应的数学对象：RooRealVar表示一个变量，RooAbsReal表示一个函数，RooAbsPdf表示一个概率密度函数（probability density function），等等。就算是最简单的数学函数也包含了很多对象——函数本身与其变量——RooFit模型也因此由许多对象组成。

RooRealVar x("x","x",-10,10) ;
RooRealVar mean("mean","Mean of Gaussian",0,-10,10);
RooRealVar sigma("sigma","Width of Gaussian",3,-10,10);
RooGaussian gauss("gauss","gauss(x,mean,sigma)",x,mean,sigma);

在gauss用到的每个变量都用几个属性进行初始化：name, title, 范围和可选的初始值。用RooRealVar描述的变量有更多的属性在这个例子中没有展现出来，例如与变量关联的对称误差以及指定变量是常量还是浮动的标志。本质上，类RooRealVar收集所有与变量有关的属性。

代码的最后一行创建了一个高斯分布的概率密度函数，由RooGaussian实现。类RooGaussian描述了所有概率密度函数的共同属性。PDF 高斯有一个名称和一个标题，就像变量对象一样，并通过构造函数中传递的引用关联到变量 x、mean 和 sigma。

2.2 模型可视化

通常我们最先想到的是看到这个模型。RooFit采取了比普通ROOT稍微正式一点的可视化方法。首先你需要定义一个“视图”，本质上是一个空的框架，包含RooRealVar中变量之一x作为横坐标轴，然后你要把你的模型gauss放进这个空白框架中，最后你再把这个视图画在ROOT TCanvas上：

RooPlot* xframe = x.frame() ; 
gauss.plotOn(xframe) ;      
xframe->Draw();            

Figure 1 - 高斯pdf

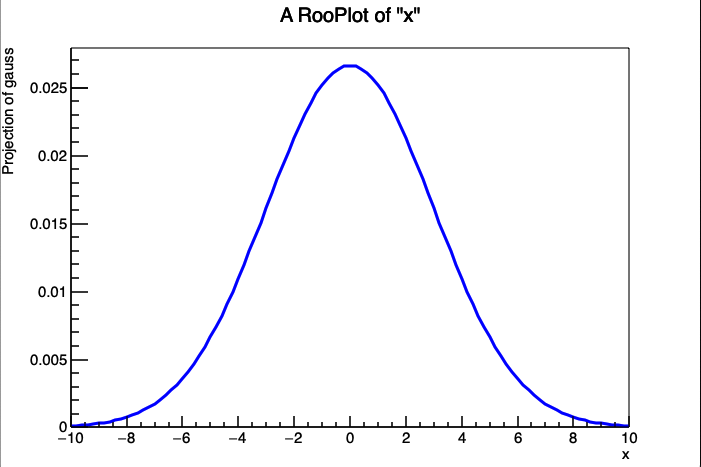
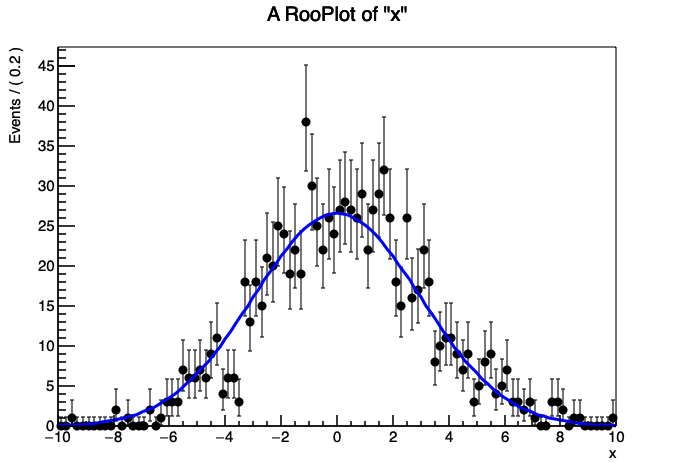
结果看图1。需要注意的是，在定义或创建一个视图的时候并不需要特意去设置范围，会根据RooRealVar中定义的变量的范围自动设置，当然你也可以重新设置范围。另外，将gauss画在框架中时，也不用说明gauss是x的函数，可以在框架中找到这个信息，就很智能。

一个框架可以可视化多个对象（曲线，直方图），我们可以画两个不同sigma值的高斯曲线

RooPlot* xframe = x.frame() ; 
gauss.plotOn(xframe) ; 
sigma = 2 ; 
gauss.plotOn(xframe,LineColor(kRed)) ; 
xframe->Draw(); 

这个例子中，在画完第一个gauss图像之后，我用赋值运算符改变了RooRealVarsigma的值。第二条曲线的颜色通过添加LineColor(kRed)参数传递给plotOn()变为红色。LineColor 是“命名参数”的一个示例。命名参数贯穿整个 RooFit 的使用，它提供一种方便且可读的方式来修改一些默认值。命名参数将在后面的部分中更详细地介绍。第二个代码片段的输出如图 2 所示。

Figure 2 - 不同宽度的高斯pdf

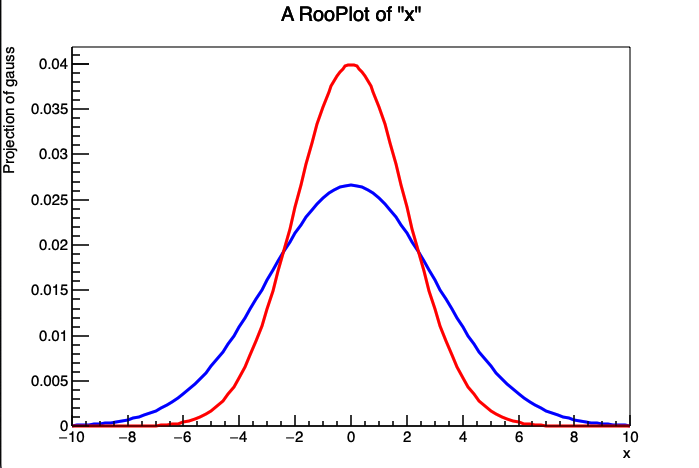
这个例子同时也展示了plotOn()方法会对PDF进行一个“冻结”的快照，如果一个pdf在画进去之后改变了形状，之前已经画进去的曲线不会发生改变。图2还展示了无论数值如何，RooGaussian总是归一化的。

Summary 1

从ROOT开发的第一天起，就决定使用一组编码约定。这样可以确保整个源代码的一致性。学习这些知识将帮助您确定正在处理的信息类型，并使您能够更好、更快地理解代码。下面是一些ROOT中的编码约定

类以 T 开头：**TLine、TTree**
非类类型以 _t 结尾：Int_t
数据成员以 **f**： fTree 开头
成员函数以大写字母开头：Loop（）
常量以 k 开头：kInitialSize、kRed

同样的在RooFit的类也会有特殊的开头——都会以Roo为开头，因此如果你在后续的学习中看到这样的函数就可以了解他是在RooFit中的函数，你可以在ROOT: RooGaussian Class Reference (cern.ch)中找到对应函数的意思和使用方法，也可以在侧边栏中找到别的成员函数，或者在右上角搜索。活用这个网页你就能成为大师！

RooGaussian::RooGaussian (const char * name, const char * title, RooAbsReal & _x, RooAbsReal & _mean, RooAbsReal & _sigma)

RooRealVar::RooRealVar (const char * name,const char * title, double minValue, double maxValue,const char * unit = “” )

RooRealVar::RooRealVar (const char * name,const char * title, double value, double minValue, double maxValue,const char * unit = “” )

RooRealVar x("x","x",-10,10); //设置自变量x，并设置定义域为[-10,10]
RooRealVar mean("mean","Mean of Gaussian",0,-10,10); //设置参数
RooRealVar sigma("sigma","Width of Gaussian",3,-10,10);
RooGaussian gauss("gauss","gauss(x,mean,sigma)",x,mean,sigma); //给RooGaussian传入三个参数，自变量x，中心值mean，宽度sigma
RooPlot* xframe = x.frame();	//创建一个以x这个变量为坐标的空坐标图，这个会直接获取你之前设置的x变量的范围定义你的坐标的范围，这里就是 -10～10
gauss.plotOn(xframe);	//将你之前创建的gauss函数画到你的坐标图中
xframe->Draw();	//将你这个图通过TCanvas“打印”出来  
sigma = 2;	
gauss.plotOn(xframe,LineColor(kRed)) ; 
xframe->Draw(); 

Summary 1 - 构建一个高斯分布的概率密度函数

Note 1

• 概率密度函数（Probability Density Function，PDF）是用于描述连续型随机变量的概率分布的函数。 随机变量 X 落在区间 [a, b] 的概率是：$P(a \leq X \leq b) = \int_a^b f_X(x) , dx$，并且还需要满足归一性和非负性。

• 对于一个函数来说，需要自变量x和参数，对于自变量来说你需要设定一个范围，也就是函数的定义域，而对于参数来说，因为你需要用这个函数去拟合一些数据，那么就不可能一开始就确定这个函数，而是给他一个大致的范围让他去拟合，这个范围还需要根据你的拟合结果进行调整，也就是调参的过程。

2.3 输入数据

通常来说，数据有两类：未分bin的，用ROOT中的TTree类表示，和分bin的，用ROOT中的TH1，TH2，TH3表示。RooFit可以处理这两种数据。用做统计身高做例子的话，unbinned 就是把每位同学的身高都记录下来，binned 就是画成条形统计图，分为不同区间去计数，每个区间就是一个bin。

2.3.1 分bin的数据（直方图）

在RooFit中，分bin的数据由RooDataHist类表示，你可以将任何ROOT直方图的内容导入到RooDataHist对象中

TH1* hh = (TH1*) gDirectory->Get("ahisto");
RooRealVar x("x","x",-10,10);
RooDataHist data("data","dataset with x",x,hh);

note：代码从当前目录 (gDirectory) 中获取名为 “ahisto” 的直方图，并将其强制转换为 TH1* 类型的指针。在ROOT中，TH1 是表示一维直方图的类。

创建了一个名为 “data” 的 RooDataHist 对象。它表示一个数据集，可以在RooFit中用于拟合或其他统计分析。
数据集用名称 “data” 和标题 “dataset with x” 构建。
此数据集根据变量 “x”（我们之前定义的变量）进行分箱，并使用先前获得的直方图 hh 填充。这意味着 hh 中的值将用于填充数据集的箱子。

当你导入ROOT直方图的时候，原直方图的bin是如何定义的同样也被导入了。RooDataHist比普通直方图更进一步的是，它将直方图的内容和一个或多个RooRealVar类型的RooFit变量关联起来。通过这种方式，它总知道直方图中存储了什么样的数据。

RooDataHist可以和gauss函数一样被plotOn在画布上。

RooPlot* xframe = x.frame() ; 
data.plotOn(xframe) ; 
xframe->Draw() 

2.3.2 未分bin的数据（树trees）

未分bin的数据可以以同样的方式导入到RooFit，并存储到RooDataSet的类中

TTree* tree = (TTree*) gDirectory->Get("atree");
RooRealVar x("x","x",-10,10);
RooDataSet data("data","dataset with x",tree,x);

在这个例子中，假设 tree 有一个名为“x”的分支，因为 RooDataSet 构造函数将从与作为参数传递的 RooRealVar 同名的树分支中导入数据。RooDataSet 可以从类型为 Double_t、Float_t、Int_t、UInt_t 和 Bool_t 的分支导入数据，用于一个 RooRealVar 可观测量。如果分支不是 Double_t 类型，则数据将转换为 Double_t，因为这是 RooRealVar 的内部表示形式。无法从数组分支（如 Double_t[10]）导入数据。可以将整数类型的数据作为离散值观测量导入到 RooFit 中，这在第8章中会更详细地解释。

绘制未分 bin 的数据与绘制分 bin 的数据类似，不同之处在于现在您可以以任何您喜欢的 binning 来显示它，默认情况下是100个bins，下面设置了25个bins的情况。

RooPlot* xframe = x.frame();
data.plotOn(frame,Binning(25));
frame->Draw();

2.3.3 working with data

在一般情况下，在RooFit中处理分组数据和未分组数据非常相似，因为RooDataSet（用于未分组数据）和RooDataHist（用于分组数据）都继承自一个共同的基类RooAbsData，该基类定义了一个通用的抽象数据样本接口。除少数例外，所有RooFit方法都接受抽象数据集作为输入参数，使得分组和未分组数据可以互换使用。本节中的示例始终处理一维数据集。然而，RooDataSet和RooDataHist都可以处理任意维数的数据。在接下来的章节中，我们将重新讨论数据集并解释如何处理多维数据。

Summary 2

下载测试用的root文件chapt2.root 里面包含了两种类型的数据：

$ root -l chapt2.root 
root [0] 
Attaching file chapt2.root as _file0...
(TFile *) 0x12758ae30
root [1] .ls
TFile**         chapt2.root
 TFile*         chapt2.root
  KEY: RooDataSet       unbinnedData;1  Generated From gaussian PDF
  KEY: TH1F     binnedHist;1    Binned Histogram of X

RooRealVar x("x", "x", -10, 10);
TFile *file = TFile::Open("./chapt2.root"); //打开root文件
TH1F *hist = (TH1F*)file->Get("binnedData"); //从文件中获取名为 "binnedHist" 的 TH1F 对象
RooDataHist binnedData("binnedData", "binnedData", x, hist);
TCanvas* c1 = new TCanvas("c1", "binned Data", 800, 600);
c1->cd();
RooPlot* x1frame = x.frame();
binnedData.plotOn(x1frame); //生成这个数据的时候的bin是20
x1frame->Draw();

TCanvas* c2 = new TCanvas("c2", "unbinned Data", 800, 600);
c2->cd();
RooDataSet* unbinnedData = (RooDataSet*)file->Get("unbinnedData");  // 从文件中获取名为 "unbinnedData" 的 RooDataSet 对象
RooPlot* x2frame = x.frame();
unbinnedData->plotOn(x2frame,Binning(40),MarkerColor(kRed)); //如果不设置bin的话默认画出的图的bin是100
x2frame->Draw();

Summary 2 - 画出binned和unbinned的数据

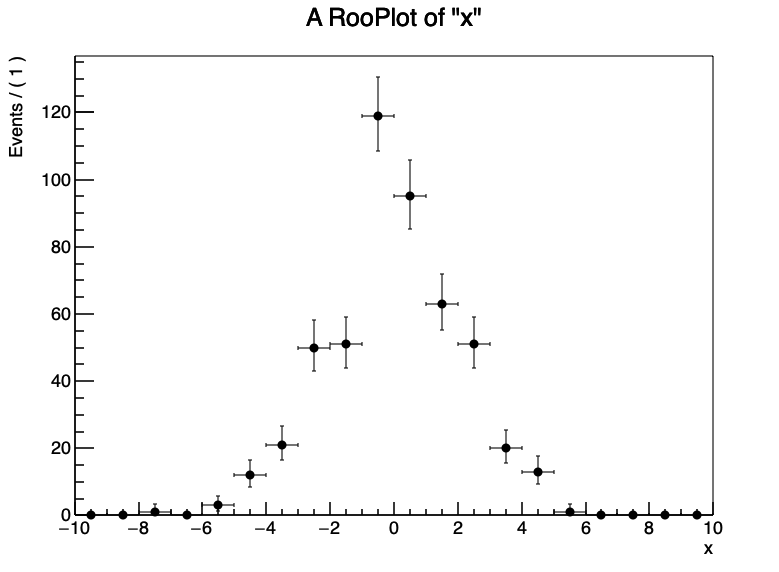
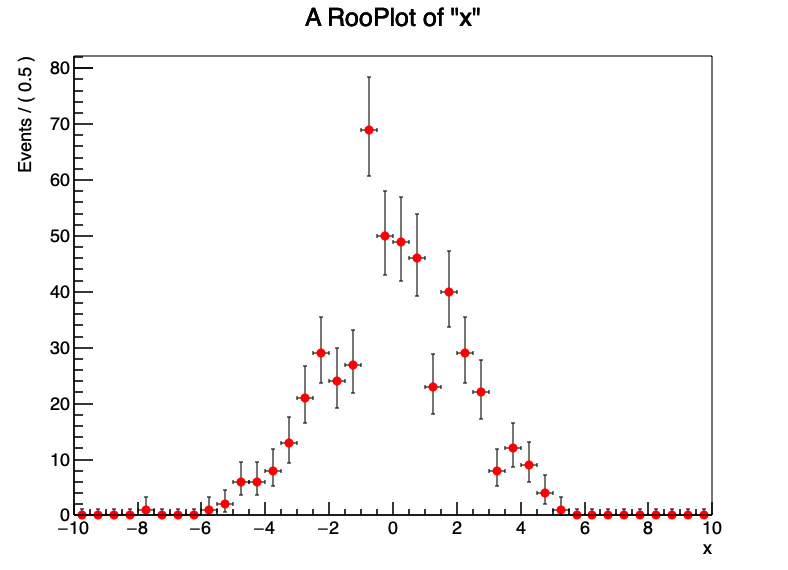
你也可以用下面的生成程序，自定义生成出你自己的root数据文件play一下

RooRealVar x("x", "x", -10, 10);
RooRealVar mean("mean", "mean of gaussian", 0, -10, 10);
RooRealVar sigma("sigma", "width of gaussian", 2, 1, 3);

// Create Gaussian PDF
RooGaussian gauss("gauss", "gaussian PDF", x, mean, sigma);

// Generate unbinned data
RooDataSet* data = gauss.generate(x, 500);

// Generate binned data
TH1F* binnedData = new TH1F("binnedData", "Binned Histogram of X", 20, -10, 10);
data->fillHistogram(binnedData, RooArgList(x));

// Create a ROOT file to save the datasets
TFile outFile("./output.root", "RECREATE");

// Write datasets to the file
data->Write("unbinnedData");
binnedData->Write("binnedData");

// Close the file
outFile.Close();

Note 2

• 对于unbinned的数据自然能随意设置bin的数量，但对于binne的数据你只能用Rebin()来合并并减少bin的数量，而不能设置更多的bin，比如Rebin(2)就代表着每两个原始 bin 合并成一个新 bin
• 当我们想进行一些精细的拟合的时候往往需要unbinned的拟合，因为binned的数据会丢失部分数据细节，但相对的，拟合速度也会下降
• unbinned的数据按道理来说像是分得无限细的binned的图，因此画出直方图的时候并不会这样操作，而是给他一个默认的bin值，从而更好地显示unbinned的数据。但是在拟合的时候还是会一个个数据点进行拟合。
• 如果你仔细看画出来的图你会发现，在低统计下的误差棒不是对称的。RooFit 默认显示泊松统计的 68% 置信区间，通常是不对称的，尤其是在低统计量下，如果直方图内容来自泊松过程，则可以更准确地反映每个箱中的统计不确定性。你可以选择将DataError(RooAbsData::SumW2)添加到data.plotOn()行来显示$\sqrt{N}$误差。这个选项只会影响数据集的可视化。

2.4 用模型拟合数据

将模型拟合到数据中涉及从模型和数据构建检验统计量——最常见的选择是χ²和负对数似然——并针对所有未固定的参数最小化该检验统计量。RooFit中的默认拟合方法是对无分箱数据进行无分箱最大似然拟合(unbinned maximum likelihood fit)，对分箱数据进行分箱最大似然拟合(binned maximum likelihood fit)。

无论哪种情况，测试统计量都是由RooFit计算的，并且测试统计量的最小化是通过ROOT中的TMinuit实现的MINUIT来进行最小化和误差分析的。整个拟合过程的易用高级接口由类RooAbsPdf的fitTo()方法提供：

gauss.fitTo(data)

这条命令从高斯函数和给定的数据集中构建一个-log(L)函数，将其传递给MINUIT，MINUIT对其进行最小化并估计高斯参数的误差。fitTo()方法的输出在屏幕上产生熟悉的MINUIT输出：(注：新版本的root的拟合输出样式发生了变化，但输出内容没有变化)

Figure 3 - 拟合输出

拟合结果——新的参数值及其误差——会传回到表示高斯参数的RooRealVar对象中，如下面的代码片段所示：

mean.Print() ;
RooRealVar::mean: -0.940910 +/- 0.030400
sigma.Print() ;
RooRealVar::sigma: 3.0158 +/- 0.022245

因此，之后绘制的高斯函数将反映拟合后的新形状。现在我们在一个框架上绘制数据和拟合函数：

RooPlot* xframe = x.frame() ;
data.plotOn(xframe) ;
model.plotOn(xframe) ;
xframe->Draw()

请注意，PDF 的归一化（本质上归一化为一）会自动调整为图中事件的数量。RooFit 的一个强大功能和其创建的主要原因之一是拟合调用对binned data和unbinned data都有效。在后一种情况下，会执行unbinned的最大似然拟合。unbinned的 -log(L) 拟合在统计上比binned拟合更有力（即，您将获得更小的均值误差），并且避免了由选择分组定义引入的任意性。这些优势在拟合小数据集和多维数据集时尤为明显。所以使用fitTo()的时候，无论数据是binned还是unbinned都能很好的拟合出来。

拟合接口高度可定制。例如，如果您想在拟合中固定一个参数，只需将其指定为 RooRealVar 参数对象的一个属性，那么这个代码片段：

mean.setConstant(kTRUE) ;
gauss.fitTo(data) ;

将参数 mean 固定为当前值重复拟合。同样，您可以选择将浮动参数限定在允许值范围内：

sigma.setRange(0.1, 3) ;
gauss.fitTo(data) ;

所有这些拟合配置信息都会自动传递给 MINUIT。可以通过传递给 fitTo() 命令的可选命名参数来控制 MINUIT 的高级方面。这个示例启用 MINOS 方法来计算不对称误差，并将 MINUIT 的详细级别设置为最低值：

gauss.fitTo(data, RooFit::Minos(true), RooFit::PrintLevel(-1)) ;

2.4.1 范围拟合

通过同样的接口可以影响似然函数的构建方式。要将似然（以及拟合）限制在指定范围内的事件子集上，可以这样做：

gauss.fitTo(data, Range(-5, 5)) ;

随后对该拟合的绘图默认只会显示拟合范围内的曲线。

关于拟合中似然函数的构建、进阶使用选项以及 $\chi^2$ 拟合的构建细节将在第12章中详细介绍。所有可用的 fitTo() 命令参数的参考指南见附录E以及方法 RooAbsPdf::fitTo() 的在线代码文档。

2.5 从模型生成数据

所有 RooFit 的概率密度函数 (p.d.f.) 都有一个通用接口，用于从其分布中生成事件。各种从分布中采样事件的技术已实现并在附录A中描述。RooAbsPdf 的内部逻辑会自动为每个使用案例选择最有效的技术。

最简单的形式中，可以从 p.d.f. 生成一个 RooDataSet，如下所示：

RooDataSet* data = gauss.generate(x, 10000) ;

这个示例创建了一个包含 10000 个事件的 RooDataSet，这些事件的可观测量 x 是从 p.d.f. gauss 中采样的。

2.6 参数和可观测量

在本章的简单示例中，我们一直使用高斯概率密度函数（p.d.f.），并且明确假设变量 $x$ 是可观测量，而变量mean和sigma是我们的参数。这一区分非常重要，因为它直接关系到对象的函数表达式：概率密度函数相对于其可观测量是单位归一化的，但相对于其参数则不是。

然而，RooFit 的 p.d.f 类本身在参数和可观测量之间没有固有的静态区分概念。这乍看之下可能令人困惑，但为我们在构建复合对象时提供了必要的灵活性。参数和可观测量之间的区分总是有的，但它是从每个使用上下文中动态产生的。以下示例展示了如何将高斯函数用作可观测量均值的 p.d.f.：

RooDataSet* data = gauss.generate(mean,1000);
RooPlot* mframe = mean.frame();
data->plotOn(mframe);
gauss.plotOn(mframe);

鉴于高斯函数的数学表达式在 $x$ 和 $m$ 的互换下是对称的，因此不出所料，这在以 $x$ 和 $\sigma$ 为参数时，得到的是一个以 $m$ 为可观测量的高斯分布。沿着同样的思路，也可以将高斯函数用作 $\sigma$ 的 p.d.f.，以 $x$ 和均值为参数。在许多情况下，不需要明确说明哪些变量是可观测量，因为其定义是从使用上下文中隐含地得出的。具体来说，只要一个使用上下文同时涉及 p.d.f. 和数据集，可观测量的隐含和自动定义是那些同时出现在数据集和 p.d.f. 定义中的变量。这种自动定义在拟合中很有效，因为拟合涉及一个显式的数据集，但也适用于绘图：RooPlot 框架变量始终被认为是可观测量。在其他所有涉及区分的上下文中，必须手动提供哪些变量被视为可观测量的定义。这就是为什么调用 generate() 时必须在每次调用中指定你认为的可观测量。

RooDataSet* data = gauss.generate(x,10000);

然而，在高斯函数的所有三种可能的用例中，它相对于（隐含声明的）可观测量都是一个适当归一化的概率密度函数。这突显了 RooFit “动态可观测量”概念的重要后果：RooAbsPdf 对象没有唯一的返回值，它取决于可观测量的局部定义。通过在 RooAbsPdf::getVal() 中的一个显式的事后归一化步骤实现了这种功能，这个步骤对于每种可观测量的定义是不同的。

Double_t gauss_raw = gauss.getVal(); // 未归一化的原始值
Double_t gauss_pdfX = gauss.getVal(x); // 用作 x 的 p.d.f 时的值
Double_t gauss_pdfM = gauss.getVal(mean); // 用作 mean 的 p.d.f 时的值
Double_t gauss_pdfS = gauss.getVal(sigma); // 用作 sigma 的 p.d.f 时的值

2.7 计算模型上的积分

在 RooFit 中，概率密度函数（p.d.f.）和函数的积分被表示为独立的对象。因此，与其将积分定义为一个动作，不如说积分是通过一个继承自 RooAbsReal 的对象来定义的，其值是通过积分操作计算得到的。这样的对象可以通过 createIntegral() 方法或 RooAbsReal 来构造。

例如：

RooAbsReal* intGaussX = gauss.createIntegral(x);

任何 RooAbsReal 函数或 RooAbsPdf 都可以通过这种方式进行积分。注意，对于 p.d.f.s，上述配置会对 gauss 的原始（未归一化）值进行积分。实际上，gauss 的归一化返回值 gauss.getVal(x) 恰好是 gauss.getVal() / intGaussX->getVal()。

大多数积分由 RooRealIntegral 类的对象表示。构造此类时，会确定执行积分请求的最有效方法。如果被积分函数支持对所请求的可观测量进行解析积分，则会使用解析实现【5】；否则，将选择数值技术。实际的积分并不是在构造时进行的，而是在调用 RooRealIntegral::getVal() 时按需进行。一旦计算出来，积分值会被缓存，并在积分参数的值发生变化或者（一个或多个）积分可观测量的归一化范围发生变化时失效。

你可以通过打印积分对象来检查选择的积分策略：

intGaussX->Print("v");

输出示例：

--- RooRealIntegral ---
Integrates g[ x=x mean=m sigma=s ]
operating mode is Analytic
Summed discrete args are ()
Numerically integrated args are ()
Analytically integrated args using mode 1 are (x)
Arguments included in Jacobian are ()
Factorized arguments are ()
Function normalization set <none>

这一输出说明了以下几点：

• 被积分的函数 $ g $ 和涉及的参数 $ $x$, $mean$, $sigma$ $。
• 操作模式为解析积分（Analytic）。
• 无需求和的离散参数。
• 无需数值积分的参数。
• $ x $ 参数使用了模式 1 的解析积分。
• 雅可比矩阵中包含的参数为空。
• 无需因式分解的参数。
• 无设置的函数归一化。

2.7.1 归一化概率密度函数(p.d.f.)

也可以构造归一化p.d.f.的积分：

RooAbsReal* intGaussX = gauss.createIntegral(x,NormSet(x)) ;

这个例子并没有太大实际用途，因为它总是返回1，但使用相同的接口，也可以在观测变量的预定义子区间上进行积分，

x.setRange("signal",-2,2) ;
RooAbsReal* intGaussX = gauss.createIntegral(x,NormSet(x),Range("signal")) ;

以提取模型在“信号”区间内的部分。诸如“信号”之类的命名区间的概念将在第3章和第7章详细阐述。归一化p.d.f.积分的返回值自然位于[0,1]范围内。

2.7.2 累积分布函数

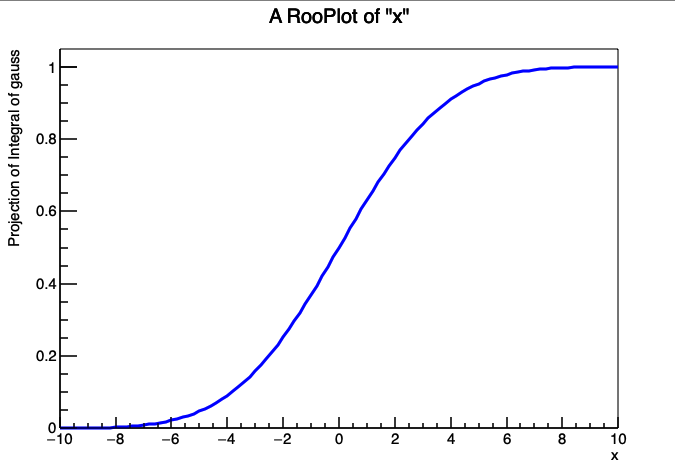
积分p.d.f.的一种特殊形式是累积分布函数（c.d.f.），其定义如下，并且可以通过专门的方法createCdf()从任何p.d.f.构造：

RooAbsReal* cdf = pdf->createCdf(x) ;

对于这种形式的积分，createCdf()相对于createIntegral()的优势在于前者能够更有效地处理需要数值积分的p.d.f.：createIntegral()在一个或多个参数变化后会从头开始重新计算整个数值积分，而createCdf()则会缓存数值积分采样阶段的结果，只重新计算求和部分。有关积分和累积分布函数的更多细节见附录C。

Summary 3

RooRealVar x("x","x",-10,10);
RooRealVar mean("mean","mean",0,-10,10);
RooRealVar sigma("sigma","sigma",3,-10,10);
RooGaussian gauss("gauss","gauss",x,mean,sigma);
RooDataSet *data= gauss.generate(x,1000);

//mean.setConstant(kTRUE); //设置mean为固定值进行拟合
//sigma.setRange(0.1,3); //设置sigma范围进行拟合

gauss.fitTo(*data);
// gauss.fitTo(*data, RooFit::Minos(true), RooFit::PrintLevel(-1), Range(-3,2));
//print level从-1到3输出的信息由详细到简略递减 
//Range设置x的拟合范围
//参考https://root.cern.ch/doc/master/classRooAbsPdf.html#ab0721374836c343a710f5ff92a326ff5

mean.Print();
sigma.Print();
RooPlot* xframe =x.frame();
data->plotOn(xframe);
gauss.plotOn(xframe);
// RooAbsReal* cdf=gauss.createCdf(x); //对你个pdf在x上求出累积分布函数cdf
// cdf->plotOn(xframe);
xframe->Draw();
// sigma = 2 ; 
// gauss.plotOn(xframe,LineColor(kRed)) ; 
// xframe->Draw(); 
x.setRange("signal",-2,2);
RooAbsReal* intg=gauss.createIntegral(x,NormSet(x));
RooAbsReal* intgsig=gauss.createIntegral(x,NormSet(x),Range("signal"));
std::cout<<"intg = "<<intg->getVal()<<endl;//对x全范围的积分，经过归一化之后为1:NormSet(x)
std::cout<<"intgsig = "<<intgsig->getVal()<<endl;//设置一个积分范围Range()

Figure 4 - 拟合曲线与累积积分曲线

Note 3

• 默认的随机生成的种子号是0，一般会根据时间设置种子号，这样每次生成都是不一样的。你可以使用RooRandom::randomGenerator()->SetSeed(seed)来自定义种子号，还有另外一种方式gRandom->SetSeed(seed)，前者是对RooFit中的随机数生成器进行设置，RooFit中的一些需要随机数的函数都会依赖这个值，后者是面向ROOT的全局随机数生成器，当除RooFit之外的其他库中也需要随机数生成的时候，会依赖这个seed。简单来说，后者可以包含前者，你可以使用gRandom->GetSeed()去查看当前的seed。

  TDatime* starttime=new TDatime();
  Int_t today=starttime->GetDate();
  Int_t clock=starttime->GetTime();
  Int_t seed=today+clock;
  RooRandom::randomGenerator()->SetSeed(seed);

• 你可以用RooFitResult去获取拟合的参数，这样在一些复杂的拟合过程，你可以设置一些条件，让拟合过程不断循环，直到拟合成功

  RooFitResult* fitRes=mytotal.fitTo(*data, Save());//保存拟合结果，并返回一个RooFitResult对象
  Data_edm = fitRes->edm();
  minNll = fitRes->minNll(); //Return minimized -log(L) value. 
  Data_status = fitRes->status(); //MINUIT status code
  Data_covQual = fitRes->covQual();
  //你还可以将最终拟合结果得到的参数输出到一个文件中
  std::ofstream outFile("fitresult.txt"); 
  fitRes->printMultiline(outFile, 0, kTRUE, "");
  
  if(Data_edm<0.001 && Data_status==0 && Data_covQual==3) {...}//设置拟合结果需要满足的条件

  1. edm (Estimated Distance to Minimum):

     • edm 是一个衡量拟合收敛性的指标。它表示当前拟合参数估计值与最小值之间的距离。较小的 edm 值表示拟合更接近最小值。通常，edm 值小于某个阈值（例如 1e-3 或 1e-4）表示拟合已经收敛。

  2. minNll (Minimized Negative Log-Likelihood):

     • minNll 是最小化的负对数似然值。它表示在拟合过程中找到的最佳参数估计值对应的负对数似然值。较小的 minNll 值表示拟合模型更好地描述了数据。通常用来计算置信度。

  3. status (MINUIT Status Code):

     是 MINUIT 拟合的状态代码。它表示拟合过程的状态。常见的状态代码包括：

     • 0：拟合成功。
     • 1：拟合未收敛。
     • 2：达到最大函数调用次数。
     • 3：达到最大参数步长。
     • 4：Hesse 矩阵计算失败。
     • 5：Hesse 矩阵计算成功，但拟合未收敛。

  4. covQual (Covariance Matrix Quality):

     是协方差矩阵的质量指标。它表示拟合参数的不确定性估计的质量。常见的质量代码包括：

     • -1：协方差矩阵未计算。
     • 0：协方差矩阵计算失败。
     • 1：协方差矩阵计算成功，但质量较差。
     • 2：协方差矩阵计算成功，质量一般。
     • 3：协方差矩阵计算成功，质量较好。

3 信号和背景 – 复合模型介绍

3.1 简介

数据模型通常用于描述包含多种事件假设的样本，例如信号和（一个或多个类型的）背景。为了描述这种性质的样本，可以构建一个复合模型。对于事件假设‘信号’和‘背景’，复合函数M(x)可以通过描述信号的函数S(x)和描述背景的函数B(x)构建，如下所示：

$ M(x) = fS(x) + (1 - f)B(x) $

在这个公式中，$ f $ 是样本中信号事件的比例。多个假设的通用表达式为：

$ M(x) = \sum_{i=1}^{N-1} f_i F_i(x) + \left(1 - \sum_{i=1}^{N-1} f_i \right) F_N(x) $

这种方式添加p.d.f.的一个特性是，M(x)不需要特意地归一化为1：如果S(x)和B(x)都是归一化为1的，那么通过这种构造，M(x)也是归一化的。RooFit提供了一个特殊的‘加法运算符’p.d.f.在RooAddPdf类中，以简化构建和使用这种复合p.d.f.。

3.1.1 扩展似然方法(extended likelihood)

测量结果通常以事件数而非事件比例的形式引用，因此，直接用信号和背景事件的数量而不是信号事件的比例（和总事件数）来表示数据模型是很有用的。具体表达如下：

$M_E(x) = N_S S(x) + N_B B(x) $

在这个表达式中 $M_E(x)$ 不是归一化为1，而是归一化为 $N_S + N_B = N$ ，即数据样本中的事件总数。因此，这不是一个严格的概率密度函数，而是两个表达式的简写：分布的形状和期望事件数。

$M(x) = \left(\frac{N_S}{N_S + N_B}\right) S(x) + \left(\frac{N_B}{N_S + N_B}\right) B(x) $

$ N_\text{Expected } = N_S + N_B $

在扩展似然方法中，可以联合约束这些表达式：

$-\log L(p) = -\sum_{\text{data}} \log M(x_i) - \log, \text{Poisson}( N_{\text{expected}}, N_{\text{expected}}) $

在RooFit中，普通的加和( $ N_{\text{coef}} = N_{\text{pdf}} - 1 $ ) 和扩展似然加和 ( $ N_{\text{coef}} = N_{\text{pdf}} $ ) 都由运算符类RooAddPdf表示，后者会自动构建扩展似然项。

3.2 构建具有系数的复合模型

我们首先从简单（非扩展）复合模型的描述开始。以下是使用分数系数通过RooAddPdf构建复合概率密度函数（PDF）的一个简单示例。

RooRealVar x("x", "x", -10, 10);
RooRealVar mean("mean", "mean", 0, -10, 10);
RooRealVar sigma("sigma", "sigma", 2, 0., 10.);
RooGaussian sig("sig", "signal p.d.f.", x, mean, sigma);

RooRealVar c0("c0", "coefficient #0", 1.0, -1., 1.);
RooRealVar c1("c1", "coefficient #1", 0.1, -1., 1.);
RooRealVar c2("c2", "coefficient #2", -0.1, -1., 1.);
RooChebychev bkg("bkg", "background p.d.f.", x, RooArgList(c0, c1, c2));

RooRealVar fsig(“fsig”,”signal fraction”,0.5,0.,1.);

// model(x) = fsig*sig(x) + (1-fsig)*bkg(x)
RooAddPdf model("model", "model", RooArgList(sig, bkg), fsig);

在这个示例中，我们首先构建一个高斯概率密度函数(sig)和一个平坦的背景概率密度函数(bkg)，然后使用信号分数(fsig)将它们加在一起构成模型。请注意，使用容器类RooArgList来作为函数的单一参数传递对象列表。RooFit有两个容器类：RooArgList和RooArgSet。每个容器类可以包含任意数量的RooFit值对象，即任何继承自RooAbsArg的对象，如RooRealVar、RooAbsPdf等。区别在于列表list是有序的，可以通过位置引用（第2个，第3个等）访问元素，并且可以包含多个同名对象，而集合set是无序的，但要求每个成员有唯一的名称。

RooAddPdf实例可以将任意数量的成分相加，要用两个系数添加三个概率密度函数，可以写成：

// model2(x) = fsig*sig(x) + fbkg1*bkg1(x) + (1-fsig-fbkg)*bkg2(x) 
RooAddPdf model2("model2","model2",RooArgList(sig,bkg1,bkg2), RooArgList(fsig,fbkg1)) ;

要构建一个非扩展的概率密度函数，其中系数为小于1的分数并且他们的和必然为1，那么系数的数量应总是比概率密度函数的数量少一个。

3.2.1 使用RooAddPdf递归

请注意，RooAddPdf的输入p.d.f.不需要是基本的p.d.f.，它们本身可以是复合p.d.f.。

// 构造第三个pdf bkg_peak
RooRealVar mean_bkg("mean_bkg","mean",0,-10,10);
RooRealVar sigma_bkg("sigma_bkg","sigma",2,0.,10.);
RooGaussian bkg_peak("bkg_peak","peaking bkg p.d.f.",x,mean_bkg,sigma_bkg);

// 首先将sig和peak以fpeak的比例相加
RooRealVar fpeak("fpeak","peaking background fraction",0.1,0.,1.);
RooAddPdf sigpeak("sigpeak","sig+peak",RooArgList(bkg_peak,sig),fpeak);

// 然后将(sig+peak)以fbkg的比例与bkg相加
RooRealVar fbkg("fbkg","background fraction",0.5,0.,1.);
RooAddPdf model("model","bkg+(sig+peak)",RooArgList(bkg,sigpeak),fbkg);

最终的p.d.f.模型表示如下表达式：
$M(x) = f_{\text{bkg}} B(x) + (1 - f_{\text{bkg}}) \left[ f_{\text{peak}} P(x) + (1 - f_{\text{peak}}) S(x) \right] $

也可以通过单个RooAddPdf的递归模式构建这样的递归加法公式。在这种构造模式下，系数的解释如下：
$M(x) = f_1 P_1 + (1 - f_1) \left[ f_2 P_2 + (1 - f_2) \left[ f_3 P_3 + (1 - f_3) P_4 \right] \right] $

例如，要构建与上面模型对象功能等价的模型，可以写成：

RooAddPdf model("model","recursive addition model", RooArgList(bkg, bkg_peak, sig), RooArgList(fbkg, fpeak, fsig), kTRUE);

这样，最终模型的形式与例子5中的递归加法表达式等效。
$M(x)=(f_1F_1+(1-f_1)(f_2F_2+(1-f_2)(f_3F_3+(1-f_3)(f_4F_4+(1-f_4)F_5))))$

3.3 绘制复合模型

复合p.d.f.的模块化结构允许你处理各个单独的组件。例如，可以在模型上绘制复合模型的各个组件，以可视化其结构。

RooPlot* frame = x.frame();
model.plotOn(frame);
model.plotOn(frame, Components(bkg), LineStyle(kDashed));
frame->Draw();

组件图以虚线样式绘制。有关绘图样式选项的完整概述，请参见[ROOT: TAttLine](https://root.cern.ch/doc/master/classTAttLine.html#:~:text=Learn how to use the TAttLine class to set and)。

你可以通过对象引用来识别组件，或者通过名称来识别组件：

model.plotOn(frame, Components("bkg"),LineStyle(kDashed)) ;

如果你的绘图代码无法访问组件对象，例如，如果你的模型是在一个只返回顶级RooAddPdf对象的独立函数中构建的，那么后一种方法非常方便。

如果你想绘制多个组件的和，也可以通过两种方式实现：

model.plotOn(frame, Components(RooArgSet(bkg1, bkg2)), LineStyle(kDashed));
model.plotOn(frame, Components("bkg1,bkg2"), LineStyle(kDashed));

请注意，在后一种形式中，允许使用通配符，因此如果选择一个合适的组件命名方案，例如，可以这样做：

RooAddPdf model("model", "bkg+(sig+peak)", RooArgList(bkg, peak, bkg), RooArgList(fbkg, fpeak), kTRUE);
model.plotOn(frame, Components("bkg"), LineStyle(kDashed));
model.plotOn(frame, Components("bkg*"), LineStyle(kDashed));

如果需要，可以在逗号分隔的列表中指定多个通配符表达式。

3.4 使用复合模型

3.4.1 拟合复合模型

拟合带有分数系数的复合模型与拟合任何其他模型没有区别：

model.fitTo(data);

模型的参数包括组件p.d.f.的参数以及由加法运算符类引入的分数参数。

3.4.2 使用多个分数拟合的常见陷阱

在涉及直（非递归）加法多个组件的模型中定义分数参数的允许范围时，需要注意一些事项。如果两个组件通过一个分数相加，那么该分数的自然范围是$0,1$。但是，如果添加了多个组件，就会有多个分数。尽管将每个分数的允许范围保持在$0,1$是合法的，但这可能会导致系数之和超过1的配置，例如当$f_1 = f_2 = 0.7$时。如果发生这种情况，最后的系数（自动计算为$1 - \sum_{i=1}^{N-1} f_i$）将变为负数。

如果在拟合过程中出现这种配置，RooFit将在每次发生时打印警告消息，但只要在似然评估的每个点上RooAddPdf的返回值仍为正，就不会采取任何措施。如果你想避免这种配置，有几种选择。

一种方法是使用RooRealVar::setRange()收紧所有分数的允许范围，使它们相加时永远不会超过1。这种方法需要一些关于你拟合的分布的知识，以避免禁止最佳拟合配置。

另一种方法是使用递归加法，在这种方法中，分数值范围$0,1$的每种排列都会生成有效的正定复合pdf。这种方法改变了系数的解释，但对要建模的分布形状不做任何假设。

第三种方法是使用扩展的似然拟合，其中所有系数都明确指定，没有隐式计算的剩余分数变为负数的可能性。

3.4.3 使用复合模型生成数据

使用复合模型生成事件的接口与使用基本模型生成事件的接口相同。

// 生成10000个事件
RooDataSet* x = model.generate(x,10000);

在内部，RooFit将利用p.d.f.的复合结构，并将事件生成委托给组件p.d.f.的方法，这通常更有效。

3.5 构建扩展复合模型(extended composite models)

为了构建可以与扩展似然拟合一起使用的复合p.d.f.，需要为每个组件指定相应的系数：

RooRealVar nsig("nsig","nsignal",100,0.,10000.) ; 
RooRealVar nbkg("nbkg","nbackground",400,0.,10000.) ;
RooAddPdf model("model", "model", RooArgList(sig, bkg), RooArgList(nsig, nbkg));

在这个例子中，系数参数的允许范围已经调整为可以容纳事件计数而不是分数。从实际角度来看，简单复合模型(plain composite models)和扩展复合模型(extended composite models)之间的区别在于，扩展复合模型中的 RooAbsPdf 对象模型可以通过其成员函数 expectedEvents() 预测预期的数据事件数（即 nsig + nbkg），而简单复合模型不能。扩展复合模型形式通过将每个系数除以所有系数的总和来得到组件分数。$M(x) = \left(\frac{N_S}{N_S + N_B}\right) S(x) + \left(\frac{N_B}{N_S + N_B}\right) B(x) $

还可以构建两个或多个已经是扩展 p.d.f. 的组件 p.d.f. 的和，在这种情况下，无需提供系数来构建扩展和 p.d.f.。这些输入可以是之前构建的 RooAddPdfs（使用扩展模式选项）或通过 RooExtendPdf 实用程序 p.d.f. 扩展的普通 p.d.f.。

RooRealVar nsig("nsig", "nsignal", 100, 0., 10000.);
RooRealVar nbkg("nbkg", "nbackground", 400, 0., 10000.);
RooExtendPdf esig("esig", "esig", sig, nsig);
RooExtendPdf ebkg("ebkg", "ebkg", bkg, nbkg);
RooAddPdf model("model", "model", RooArgList(esig, ebkg));

Figure 5 - 扩展复合模型

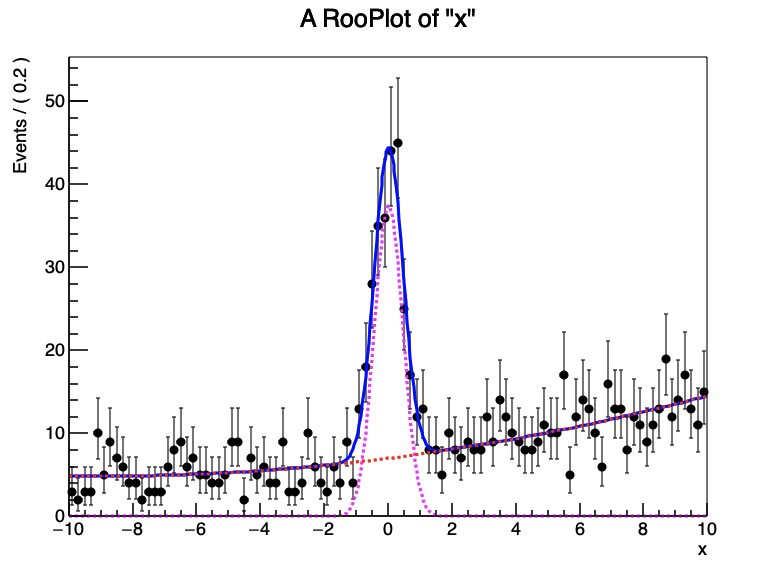
3.5.1 范围内信号事件产量

假设你对Figure 5 中模型的范围$[-2,2]$内的信号事件产量感兴趣：

你可以通过将总信号产量乘以信号 p.d.f. 形状在范围$[-2,2]$内的分数来计算这一点，但仍然需要手动传递信号产量和形状分数积分的误差到最终结果。RooExtendPdf 类提供了在预期事件数的计算中立即应用转换的可能性，以便似然函数，从而拟合结果，直接以 $N_{sig}^{Window}$ 表示，并且所有误差都会自动正确传播。

这种修改的效果是 esig 返回的预期事件数变为：

$N_{\text{sig}}^{\text{expected}} = N_{\text{sig}}^{\text{ window}} \int_{4}^{6} S(x) , dx $

这样，在最小化扩展最大似然后，nsigw 等于信号窗口中事件数的最佳估计值。通过这种方式，您可以在拟合时直接得到信号窗口内的事件数及其误差。

x.setRange("window", 4, 6);
RooAbsReal* fracSigRange = sig.createIntegral(x, x, "window");
Double_t nsigWindow = nsig.getVal() * fracSigRange->getVal();
//先计算窗口区的信号比例，再用总信号数*窗口区比例=窗口区的信号数，但不能传递误差
RooRealVar nsigw("nsigw", "nsignal in window", 500, 0, 10000.);
RooExtendPdf esig("esig", "esig", sig, nsigw, "window");

3.6 使用扩展复合模型生成事件

3.6.1 从扩展模型生成事件

一些额外的特性适用于为扩展似然形式构建的复合模型。由于这些模型预测了一定数量的事件，因此可以省略请求生成的事件数量：

RooDataSet* x = model.generate(x);

在这种情况下，将生成由概率密度函数（p.d.f.）预测的事件数量。您还可以选择通过 Extended() 参数引入泊松波动到生成的事件数量中：

RooDataSet* x = model.generate(x, Extended(kTRUE));

如果您在研究中生成了许多样本并查看拉量分布，这是非常有用的。为了使事件计数参数的拉量分布正确，生成的事件总数应存在泊松波动。关于拟合研究和拉量分布的详细内容，请参见第14章。

3.6.2 拟合

复合扩展概率密度函数（p.d.f.）只有在包含扩展似然项进行最小化时才能成功拟合，因为它们在参数化中有一个由该扩展项约束的额外自由度。如果一个概率密度函数能够计算扩展项（例如任何扩展的 RooAddPdf 对象），则扩展项会自动包含在似然计算中。您可以通过在 fitTo() 调用中添加 Extended() 参数手动覆盖此默认行为：

model.fitTo(data, Extended(kTRUE)); // 可选

3.6.3 绘图

扩展似然模型的可视化默认程序与常规概率密度函数相同：用于归一化的事件计数是添加到绘图框架中的最后一个数据集的事件计数。您可以选择覆盖此行为并使用概率密度函数的预期事件计数进行归一化，如下所示：

model.plotOn(frame, Normalization(1.0, RooAbsReal::RelativeExtended));

Summary 4

RooRealVar x("x","x",-10,10);
RooRealVar mean("mean","mean",0,-10,10);
RooRealVar sigma("sigma","sigma",0.5,0.,1.);
RooGaussian gaus("gaus","guas",x,mean,sigma);
RooRealVar c0("c0","c0",0.5,-1.,1.);
RooRealVar c1("c1","c1",0.1,-1.,1.);
RooChebychev chev("chev","chev",x,RooArgList(c0,c1));

RooRealVar c2("c2","c2",0.5,-1.,1.);
RooRealVar c3("c3","c3",0.1,-1.,1.);
RooChebychev chev2("chev2","chev2",x,RooArgList(c2,c3));

RooRealVar nsig("nsig", "signal fraction", 100, 0., 10000.);
RooRealVar nbkg("nbkg", "background fraction", 400, 0., 10000.);
RooExtendPdf egaus("egaus", "egaus", gaus, nsig);
RooExtendPdf echev("echev", "echev", chev, nbkg);
// modelE(x) = nsig/(nsig + nbkg) gaus(x) + nbkg/(nsig + nbkg) chev(x)
RooAddPdf modelE("modelE", "modelE", RooArgList(egaus, echev));

RooRealVar fsig("fsig","fsig",0.2,0,1.);
//model1(x) = fsig*gaus(x) + (1-fsig)*chev(x)
RooAddPdf model1("model1","model1",RooArgList(gaus,chev),fsig);

RooRealVar fbkg("fbkg2","fbkg2",0.2,0,1.);
// model2(x) = fsig*gaus(x) + fbkg*chev(x) + (1-fsig-fbkg)*chev2(x) 
RooAddPdf model2("model2","model2",RooArgList(gaus,chev,chev2),RooArgList(fsig,fbkg));

RooDataSet *data= model2.generate(x,1000);
model2.fitTo(*data);
RooPlot* xframe =x.frame();
data->plotOn(xframe);
model2.plotOn(xframe);
model2.plotOn(xframe, Components(gaus),LineStyle(kDashed),LineColor(6));
model2.plotOn(xframe, Components("chev2"),LineStyle(kDashed),LineColor(2));
model2.plotOn(xframe, Components("chev*"),LineStyle(kDashed),LineColor(3));//有两种component的引用方法，当你有很多个组分需要一起画的时候，加双引号可以使用通配符“*”
xframe->Draw();

Figure 5 - 画出复合pdf的不同组分

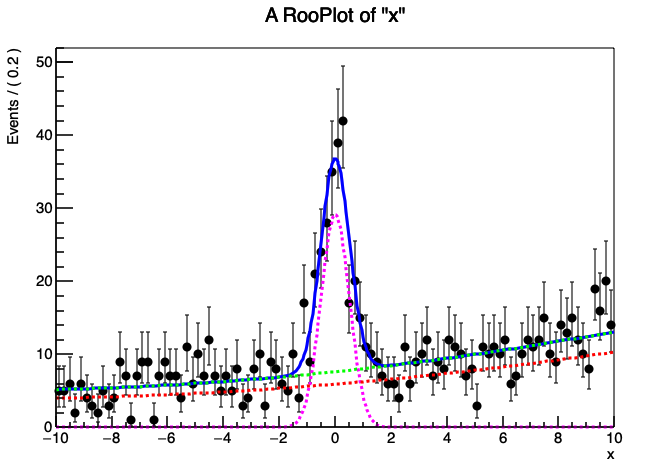
Note 4

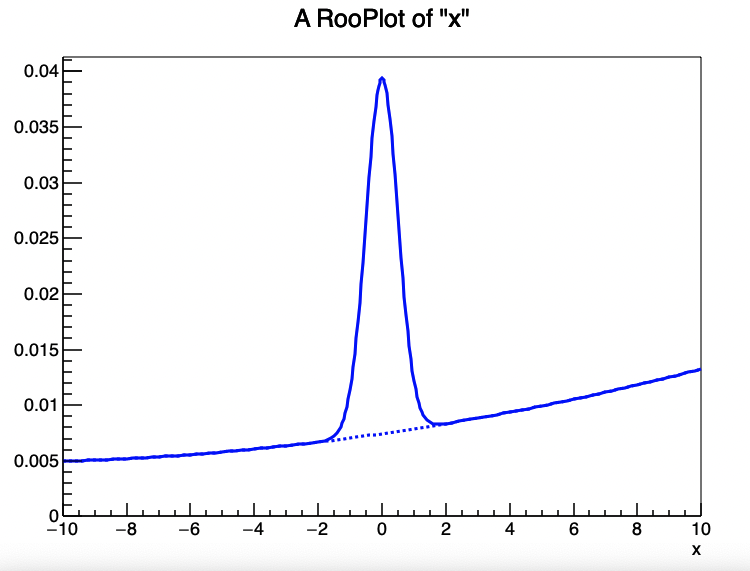
• 大多数情况下，在高能物理的数据拟合中，我们都会用Extended的模型，因为这样可以直接获取其中的事例数的多少。除此之外，使用复合模型的时候会因为你的可观测量(x)的范围发生变化而导致你的pdf形状发生改变，因为复合概率密度函数的表达式$ M(x) = \sum_{i=1}^{N-1} f_i F_i(x) + \left(1 - \sum_{i=1}^{N-1} f_i \right) F_N(x) $ 中的系数是和函数的归一化密切相关的，你设置的可观测量范围就是归一化的范围，因此范围改变的时候函数形状也会发生改变。你可以通过下面的实例感受其中的区别：

  RooRealVar x("x","x",-10,10);
  RooRealVar mean("mean","mean",0,-10,10);
  RooRealVar sigma("sigma","sigma",0.5,0.,1.);
  RooGaussian gaus("gaus","guas",x,mean,sigma);
  RooRealVar c0("c0","c0",0.5,-1.,1.);
  RooRealVar c1("c1","c1",0.1,-1.,1.);
  RooChebychev chev("chev","chev",x,RooArgList(c0,c1));
  
  RooRealVar fsig("fsig","fsig",0.2,0,1.);
  //model(x) = fsig*gaus(x) + (1-fsig)*chev(x)
  RooAddPdf model("fsig","fsig",RooArgList(gaus,chev),fsig);
  
  //按照一开始观测量设置的范围画出来的就是-10,10的范围
  RooPlot* xframe =x.frame();
  model.plotOn(xframe);
  model.plotOn(xframe, Components("chev"),LineStyle(kDashed));
  TCanvas *cv0 = new TCanvas("cv0","cv0",800,600);
  cv0->cd();
  xframe->Draw();
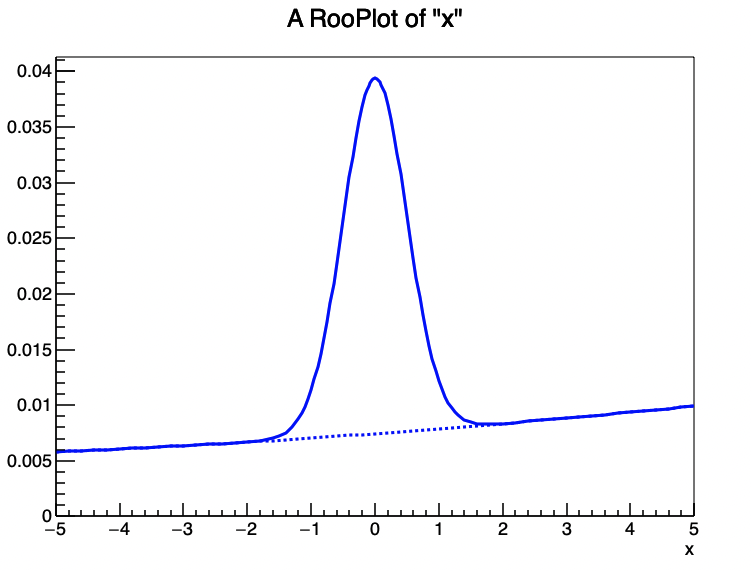
  //观测量依然是-10,10的范围，但是改变了画图的范围
  RooPlot* xframe1 =x.frame();
  model.plotOn(xframe1);
  model.plotOn(xframe1, Components("chev"),LineStyle(kDashed));
  TCanvas *cv1 = new TCanvas("cv1","cv1",800,600);
  cv1->cd();
  xframe1->GetXaxis()->SetRangeUser(-5, 5);
  xframe1->Draw();
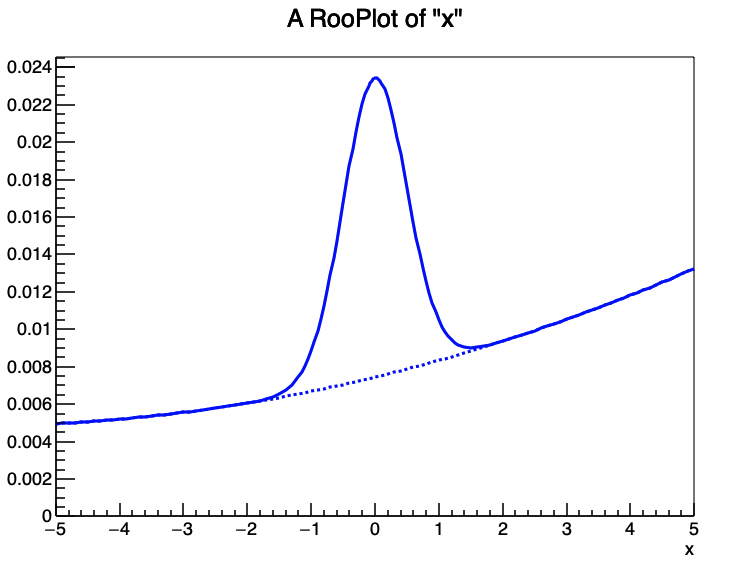
  //重新设置了观测量的范围，变为-5,5
  x.setRange(-5,5) ;
  RooPlot* xframe2 =x.frame();
  // data->plotOn(xframe);
  model.plotOn(xframe2);
  model.plotOn(xframe2, Components("chev"),LineStyle(kDashed));
  TCanvas *cv2 = new TCanvas("cv2","cv2",800,600);
  cv2->cd();
  xframe2->Draw();

Figure 6 - cv0(左)cv1(中)cv2(右)，你可以通过看曲线的最高点观察他们之间的区别

4 选择、调整和创建基本函数

我们现在详细了解 RooFit 提供的基本概率密度函数（p.d.f.），如何根据具体问题调整它们，以及如何在现有函数无法满足需求时自定义新的 p.d.f.。

4.1 RooFit 提供了哪些 p.d.f.?

RooFit 包含一个约 20 个概率密度函数的库，可以作为构建模型的基本模块。这些函数包括：基本函数(basic functions)，非参数化函数(non-parametric functions)，受物理启发的函数(physics-inspired functions)，专用于 B 物理的衰变函数(specialized decay functions for B physics)。更详细的描述可参考附录 B 的 p.d.f. 图集。

4.1.1 基本函数

以下是 RooFit 提供的基本 p.d.f. 形状：

• 高斯分布 RooGaussian 标准正态分布。

• 双分叉高斯分布 RooBifurGauss高斯分布的变体，允许独立设置均值两侧（低侧和高侧）的宽度。

• 指数分布 RooExponential 标准指数衰减分布。

• 多项式分布 RooPolynomial标准多项式形状，支持设置每个 $x^n$ 项的系数。

• 切比雪夫多项式 RooChebychev实现了第一类切比雪夫多项式。

• 泊松分布RooPoisson 标准泊松分布。

每个 p.d.f. 的形式比标准形式少一个参数，因为归一化约束要求 p.d.f. 的积分始终为 1，从而消除了控制“垂直”尺度的自由度。

4.1.2 非参数化函数

RooFit 提供了两类可以描述外部数据分布形状的非参数化方法，无需显式参数化：

• 直方图 RooHistPdf 一个表示外部 RooDataHist 直方图形状的概率密度函数（p.d.f.）。可以选择性地通过插值构造平滑函数。
• 核估计 RooKeysPdf一个表示外部无分箱数据集形状的概率密度函数（p.d.f.）。它通过一系列高斯函数的叠加来表示形状，每个高斯具有相等的面积，但宽度可变，具体取决于局部事件密度。

4.1.3 受物理启发的函数

除了基本形状外，RooFit 还实现了一系列常用于模拟物理“信号”分布的函数：

• Landau 分布 RooLandau用于参数化粒子在材料中的能量损失，没有解析形式。RooFit 使用 TMath::Landau 的参数化实现。

• 布赖特-维格纳分布（Breit-Wigner）RooBreitWigner 用于描述非相对论性布赖特-维格纳共振形状的分布。其扩展版本 Voigt 分布（类 RooVoigtian）结合了布赖特-维格纳分布和高斯分布，常用于在考虑有限探测器分辨率的情况下描述共振形状。

• Crystal Ball 分布 RooCBShape在低端带有拖尾的高斯分。传统上用于描述不变质量中的辐射能量损失效应。

• Novosibirsk 分布 RooNovosibirsk 一种修正的高斯分布，带有额外的尾参数。该尾参数会将高斯分布偏向不对称形状：一侧为长尾，另一侧为短尾。

• Argus 分布 RooArgusBG 一种经验公式，用于模拟多体衰变在接近阈值时的相空间分布。在 B 物理研究中被广泛使用。

• $D^{*\pm}-D^0$相空间分布 RooDstD0BG 一种具有单参数的经验函数。用于模拟$D^{*\pm}-D^0$不变质量差分布中的背景相空间。

这些函数为建模物理信号分布提供了强大的工具，特别是在高能物理和核物理实验中具有重要应用。

4.1.4 B 物理的专用函数

RooFit 最初为 SLAC 的 B 工厂实验 BaBar 开发，因此提供了一系列专门用于描述 介子衰变及其物理效应的概率密度函数（p.d.f.）。这些函数适用于包含混合、CP 破坏等现象的 衰变建模：

• 衰变分布 RooDecay描述: 单边或双边指数衰变分布。

• 带混合的衰变分布 RooBMixDecay 单边或双边指数衰变分布，包含$B^0$-$\bar{B}^0$ 混合效应。

• 带标准模型 CP 破坏的衰变分布 RooBCPEffDecay 单边或双边指数衰变分布，包含标准模型中的 CP 破坏效应。

• 带通用 CP 破坏的衰变分布 RooBCPGenDecay 单边或双边指数衰变分布，使用通用参数化描述 CP 破坏效应。

• 衰变至非 CP 本征态的分布 RooNonCPEigenDecay 单边或双边指数衰变分布，描述衰变到非 CP 本征态的情况，并包含通用参数化的 CP 破坏效应。

• 通用衰变分布（包括混合、CP 和 CPT 破坏） RooBDecay 最通用的 B 衰变描述，支持可选的混合、CP 破坏和 CPT 破坏效应。

这些专用函数为高能物理实验中的 衰变建模提供了灵活且强大的工具，尤其适用于涉及混合和对称性破坏研究的场景。

4.2 重新参数化现有的基本 p.d.f.

在第 3 章中提到，RooAbsPdf 类没有将变量固定为参数或观测值的内在概念。事实上，RooFit 的函数和概率密度函数（p.d.f.）对函数参数是否是变量（例如 RooRealVar）并没有强制要求。因此，可以通过将函数替代参数来修改任何现有 p.d.f. 的参数化。

以下代码示例展示了如何通过重新参数化构造一个新的 p.d.f.：

// 定义观测变量 x
RooRealVar x("x", "x", -10, 10);
// 构造第一个高斯函数 sig_left(x, mean, sigma)
RooRealVar mean("mean", "mean", 0, -10, 10);
RooRealVar sigma("sigma_core", "sigma (core)", 1, 0., 10.);
RooGaussian sig_left("sig_left", "signal p.d.f.", x, mean, sigma);
// 构造偏移函数 mean_shifted(mean, shift)
RooRealVar shift("shift", "shift", 3.0);
RooFormulaVar mean_shifted("mean_shifted", "mean+shift", RooArgSet(mean, shift));
// 构造第二个高斯函数 sig_right(x, mean_shifted, sigma)
RooGaussian sig_right("sig_right", "signal p.d.f.", x, mean_shifted, sigma);
// 构造总 p.d.f. sig = sig_left + sig_right
RooRealVar frac_left("frac_left", "fraction (left)", 0.7, 0., 1.);
RooAddPdf sig("sig", "signal", RooArgList(sig_left, sig_right), frac_left);

最终构建的 p.d.f. sig 是由两个高斯函数组成的，其中第二个高斯的均值相对于第一个高斯的均值偏移了一个固定量 shift。这种方法通过公式对象（RooFormulaVar）实现了动态参数化，提供了灵活的分布构造方式。

Figure 7 - 用`RooFormulaVar`设置一个固定的偏移量

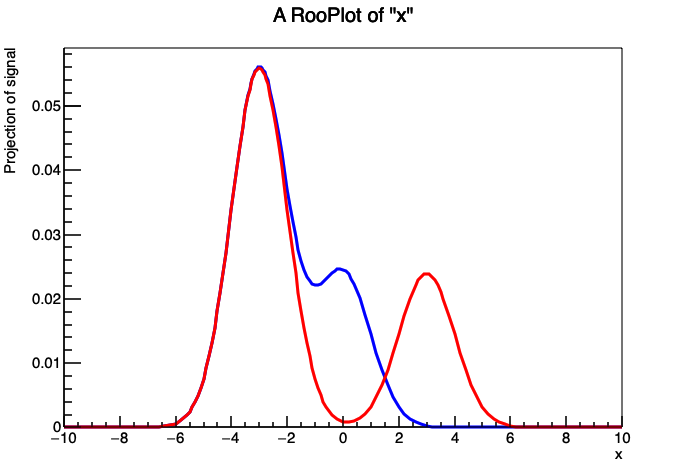
4.2.1 RooFormulaVar

RooFormulaVar 是一种可求值的实值函数，通过 ROOT 的 TFormula 引擎解释公式表达式来完成计算。例如，在上述例子中，用 mean+shift 计算右侧高斯分布的均值位置。

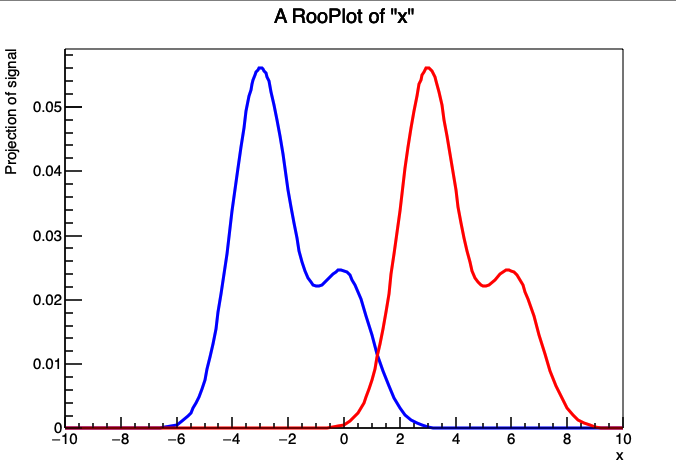
尽管复合 p.d.f. sig 的形式与两个普通高斯分布（各自独立均值）的组合没有差别，但重新参数化模型的能力提供了一些新的便利。例如，可以让均值 mean 浮动拟合，同时保持两个高斯之间的距离 shift 固定。Figure 7 展示了在上述例子中，对于 mean=-3 和 mean=3 以及 shift=3 和 shift=6 的组合情况，分别绘制出的红色和蓝色 sig 分布。

RooFormulaVar支持的表达式与 ROOT 的 TFormula 一致，包括大部分数学操作符（+、-、/、* 等）、嵌套括号以及一些基础数学和三角函数（如 sin、cos、log、abs 等）。可以通过公式表达式中变量的名称（在构造函数的第三个参数 RooArgSet 中提供）进行引用。也可以通过位置索引引用变量，例如：

RooFormulaVar mean_shifted("mean_shifted", "@0+@1", RooArgList(mean, shift));

这种方式在采用“工厂风格”编程时尤为方便，因为在编写代码时不需要知道变量的具体名称。

对于简单的数学变换，RooFit 提供了以下实用工具类：RooPolyVar实现多项式函数，RooAddition实现多个组件的加和，RooProduct实现多个组件的乘积。这些类可以满足常见的简单组合需求。如果需要更复杂的变换，可以通过编写专门的类来实现。

4.3 写一个新的p.d.f.类

如果现有的 p.d.f. 类都不符合您的需求，且没有人可以通过使用 RooFormulaVar 来进行自定义，那么编写您自己的 RooFit p.d.f. 类是非常容易的。

4.3.1 RooGenericPdf 解释型通用 p.d.f. 类

如果您的模型的公式表达式相对简单，且性能不是关键因素，您可以使用 RooGenericPdf，它会像 RooFormulaVar 一样解释您的 C++ 表达式。

RooRealVar x("x","x",-10,10) ; 
RooRealVar alpha("alpha","alpha",1.0,0.,10.) ;
RooGenericPdf g("g","sqrt(abs(alpha*x))+0.1",RooArgSet(x,alpha)) ;

RooPlot* xframe =x.frame();
g.plotOn(xframe);
alpha=1e-4 ;
g.plotOn(xframe,LineColor(2));
xframe->Draw();

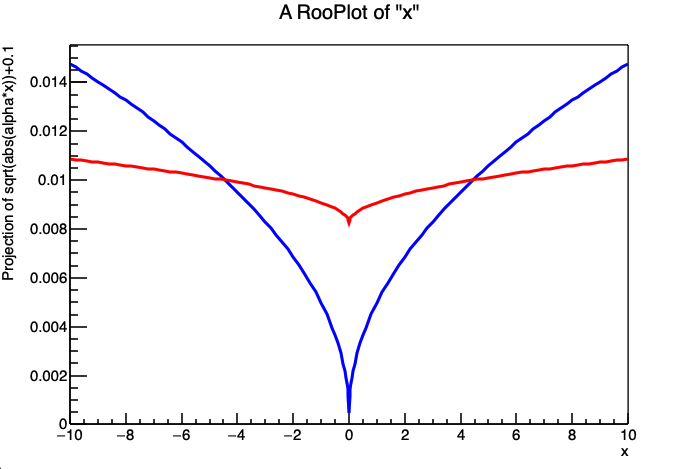
输入到 g 中的公式表达式在返回 p.d.f. g 的值之前会通过数值积分显式地进行归一化，因此不要求提供的表达式本身是归一化的。自动归一化在图 14 中得到了很好的展示，图中显示了参数 alpha 的两个值对应的 p.d.f. g。如果您的公式表达式比上述示例更复杂，您应编写一个编译后的类来实现您的函数。

Figure 8 - 用 RooGenericPdf 自定义一个pdf并且不需要特意归一化

4.3.2 RooClassFactory

实用类 RooClassFactory 简化了编写自定义 RooFit p.d.f. 类的任务，主要是将实际的 p.d.f. 表达式写出来。该类工厂有几种操作模式。最简单的操作模式是针对足够简单的函数表达式，这些表达式可以用一行代码来表示。在这种情况下，可以按如下方式编写一个完全功能的自定义 p.d.f. 类：

RooClassFactory::makePdf("RooMyPdf","x,alpha",0,"sqrt(abs(x*alpha))+0.1");

这个操作会生成两个文件，RooMyPdf.cxx 和 RooMyPdf.h，这些文件可以编译并通过 ACliC 链接以供立即使用。在 ROOT 中，可以通过以下命令加载：

root> .L RooMyPdf.cxx+

这是将原始示例用新的编译类 RooMyPdf 重写后的版本：

RooRealVar x("x","x",-10,10) ;
RooRealVar alpha("alpha","alpha",1.0,0.,10.) ;
RooMyPdf g("g","compiled class g",x,alpha) ;

如果您的函数表达式不够简单，无法用一行代码表示，您可以在请求 RooClassFactory 创建类时简单地省略表达式：

RooClassFactory::makePdf("RooMyPdf","x,alpha") ;

这会创建一个功能完全的类，并提供一个 RooAbsPdf::evaluate() 的虚拟实现。为了使其成为一个功能完整的类，您需要编辑 RooMyPdf.cxx 文件，并在类的 evaluate() 方法中插入函数表达式作为返回值，您可以使用任意数量的代码行：

Double_t RooMyPdf::evaluate() const {
  // 在此处插入基于变量参数的表达式
  return 1 ;
}

您可以将您在 makePdf() 调用中列出的所有符号作为 C++ 的 double 对象使用。由于 RooAbsPdf 对变量是否是观测量或参数没有固定的解释，因此在 evaluate() 中明确地对某个特定的观测量进行归一化没有必要或意义：evaluate() 的返回值总是在返回通过 RooAbsPdf::getVal() 之前，通过归一化积分进行后期归一化。默认情况下，这个归一化步骤是通过数值积分器完成的，但如果您知道如何在一个（或多个）观测量的选择下进行积分，您可以在 p.d.f. 中声明这个功能，并且在合适的时候会使用您的解析积分，而不是数值积分。

您可以使用不同的选项调用 RooClassFactory::makePdf()，它会为解析积分接口生成框架代码。详细信息可以在 RooClassFactory 的 HTML 类文档中找到。关于如何编写 p.d.f. 类以支持解析积分和内部事件生成处理的更多信息，参见第 14 章。

4.3.3 自定义 p.d.f 对象的实例化方法（使用 RooClassFactory）

RooClassFactory 的另一种操作模式是请求工厂立即编译并实例化一个基于给定变量对象集合的对象。例如：

RooAbsPdf* myPdf = RooClassFactory::makePdfInstance("RooMyPdf", "sqrt(abs(x*alpha))+0.1", RooArgSet(x,alpha));

需要注意的是，这种调用方式与创建 RooGenericPdf 类型对象的方式非常相似：你提供一个包含 C++ 函数表达式的字符串和一组输入变量，工厂返回一个实现该函数形状的 RooAbsPdf 实例。两者的区别在于代码生成的方式：

• RooGenericPdf：采用解释的方式。
• RooClassFactory：采用编译的方式。

具体选择哪种方式取决于使用场景：

• RooGenericPdf 方法几乎没有启动开销，但在绘图、事件生成和拟合的执行速度上会有所降低。
• RooClassFactory 方法会带来更快的执行速度，但每次宏运行时需要几秒钟的编译和链接代码的启动开销。

4.3.4 使用 RooClassFactory 编写新函数类

除了创建 p.d.f. 的框架代码，RooClassFactory 还可以为通用的实值函数生成框架代码。这些函数类是 RooFit 中继承自 RooAbsReal 的所有类。RooFormulaVar 就是一个通用实值函数的典型例子。

与 p.d.f. 不同的是，RooAbsReal 类的对象不需要归一化到 1，也可以取负值。在以下两种情况下，编译自定义的实值函数是一个很好的选择：

1. 表达式较为复杂。
2. 性能要求较高。

要为通用函数对象生成框架代码，可以使用 RooClassFactory 的 makeFunction() 方法。例如：

RooClassFactory::makeFunction("RooMyFunction", "x,b");

该代码将创建一个通用函数类的框架代码，方便用户进行进一步的自定义和优化。

Note 5

除了一些RooFit中自带的pdf，我们会用一些自定义的函数去更好地解释实验中的数据。

• 用RooFormulaVar去构建特殊的变量

  RooFormulaVar mean_shifted("mean_shifted", "mean+shift", RooArgSet(mean, shift));
  RooFormulaVar mean_shifted("mean_shifted", "@0+@1", RooArgList(mean, shift));

• 用RooGenericPdf构建简单的函数

  RooRealVar x("x","x",-10,10) ; 
  RooRealVar alpha("alpha","alpha",1.0,0.,10.) ;
  RooGenericPdf g("g","sqrt(abs(alpha*x))+0.1",RooArgSet(x,alpha));

• 用RooClassFactory构建复杂的函数，会生成对应的.h和.cxx文件，后续章节中会详细说明

  RooAbsPdf* myPdf = RooClassFactory::makePdfInstance("RooMyPdf", "sqrt(abs(x*alpha))+0.1", RooArgSet(x,alpha));

5 将一个 p.d.f. 或函数与另一个 p.d.f. 卷积

5.1 引言

在高能物理实验中，实验数据分布通常是由一个理论分布经过探测器响应函数修正后的结果。在最一般的情况下，这种分布可以用理论模型 $T(x,a) $ 描述粒子的基本物理分布和探测器响应函数$R(x,b)$ 描述探测器对粒子的测量误差或分辨率的卷积来描述：

$M(x, a, b) = T(x,a)\otimes R(x,b)= \int^{+\infty}_{-\infty} T(x, a) , R(x - x’, b) , dx’$

一个常见的例子是将 Breit-Wigner 理论模型与高斯探测器响应函数相卷积，其结果如图 9 所示。如果你想了解更多关于卷积的概念，这个视频中介绍了两种很形象的理解方式——卷积的两种可视化|概率论中的X+Y既美妙又复杂，或者参考相关书籍。

Figure 9 - Breit-Wigner 理论模型与高斯探测器响应函数卷积

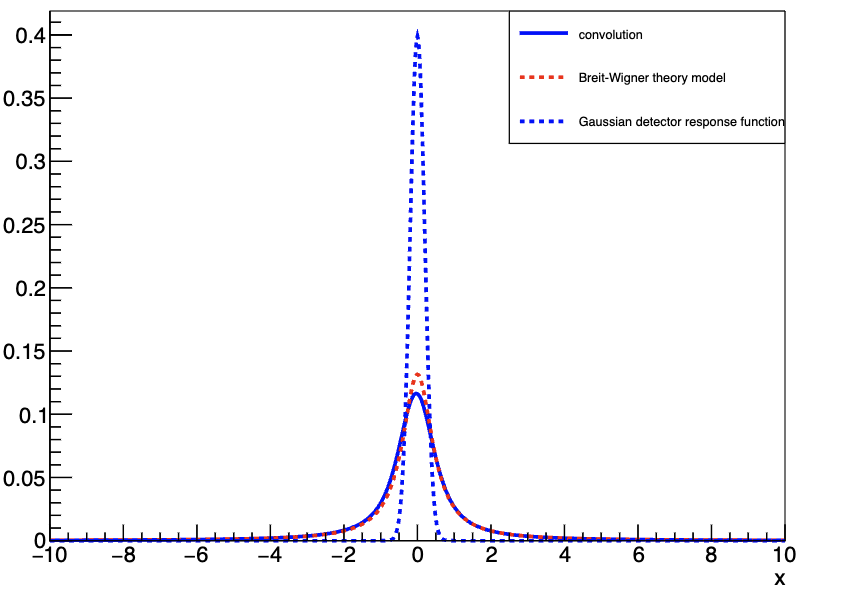
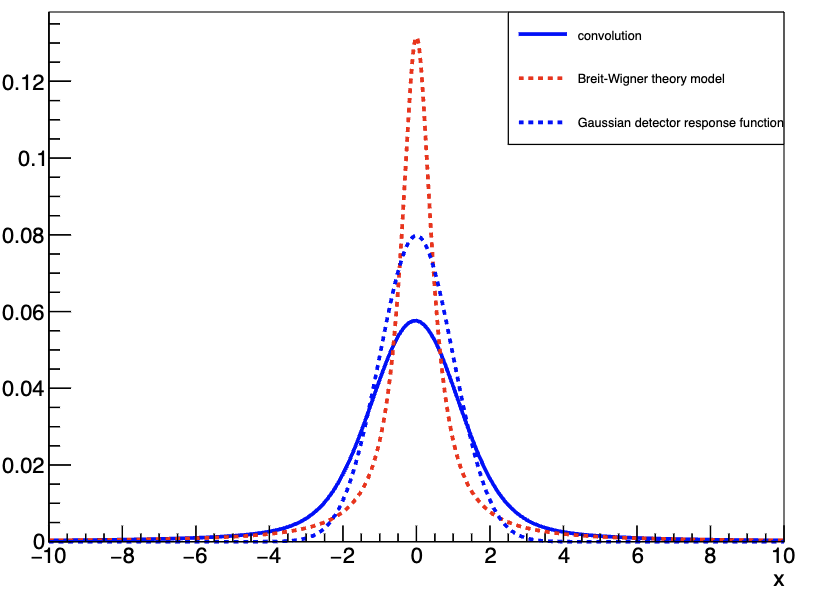
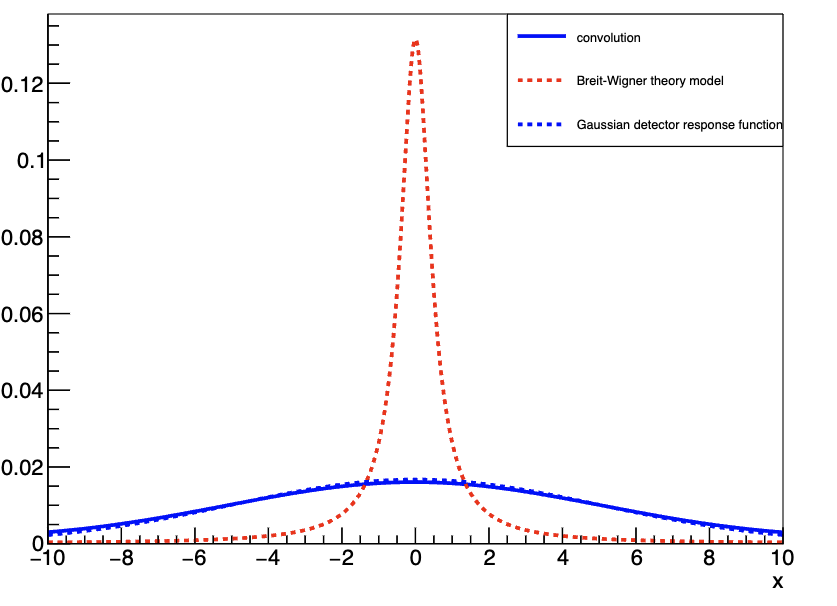
通常，所得分布可能主要由探测器响应主导，此时 M(x,a,b)可以有效地用 R(x,b)近似（图 9-左）；或者主要由理论模型主导，此时 M(x,a,b)可以有效地用 T(x,a) 近似（图 9-右）。然而，当两种函数的效应具有相当的量级时（图 9-中），可能需要显式计算卷积积分。在本章节中，我们将解释如何在 RooFit 中计算此类卷积。

5.1.1 卷积的计算

在概率密度函数中进行卷积计算通常在计算上具有一定的挑战性。仅在少数情况下，对于 $R(x)$ 和 $ T(x)$ 的特定选择，卷积分可以解析计算；对于所有其他情况，卷积积分需要在区间$[-\infty, \infty]$上进行数值积分。

此外，对于概率密度函数，还需要进行显式的归一化步骤，因为两个在有限区域上归一化的概率密度函数的卷积并不一定自身归一化。因此，对于概率密度函数 $M$ 的表达式为：

$M(x) = T(x,a)\otimes R(x,b)=\frac{\int_{-\infty}^\infty T(x, a) R(x - x’, b) dx’}{\int_{x_{min}}^{x_{max}} \int_{-\infty}^\infty T(x, a) R(x - x’, b) dx’ dx}$

该归一化过程确保 $M(x)$ 满足概率密度函数的性质，即其在定义域上的积分为 1。

5.1.2 卷积计算的多种选择

RooFit 提供了三种方法来表示卷积概率密度函数：

1. 使用傅里叶变换进行数值卷积计算。
2. 使用直接积分进行数值卷积计算。
3. 针对特定概率密度函数的解析卷积计算。

5.2 数值卷积与傅里叶变换

对于大多数应用，使用傅里叶变换空间计算的数值卷积在灵活性、精度和计算强度之间提供了最佳的权衡。为了更好地理解使用离散傅里叶变换计算卷积的特点，我们首先简要介绍一下基础数学。

5.2.1 圆卷积定理和离散傅里叶变换

圆卷积定理指出，两个系数序列$ x_i$ 和 $y_i$ 在空间域的卷积可以通过在频率域中将系数进行简单的乘法运算来计算，即：$(x \otimes y)_n \underset{F}{\Leftrightarrow}\left(x_k \cdot y_k\right)$

该定理使得我们可以在不显式计算积分的情况下计算卷积。缺点是它需要傅里叶变换和离散输入数据。然而，实际上，这些问题比在开放域上进行数值积分要更容易解决。该定理的另一个特点是，对于有限的 n，卷积观察量被视为周期性的，这在某些应用中可能是需要的，在其他情况下则可能不需要。我们稍后会回到这一点。

为了能够使用离散傅里叶变换，所有连续的输入函数必须被采样成离散的分布：

$F(x) \underset{sampling}{\Longrightarrow } x_i $

任何这样的离散分布 x_i 都可以通过傅里叶变换在频率域中表示为等数量的系数 X_i：

$X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N} k n}$

空间域的系数 x_i 和频率域的系数 X_i 通常都是复数。如果输入系数 x_i 是实数（如从概率密度函数采样时的情况），则频率域的系数 X_i 会展示对称性，即 X_{n-k} = X_k^*。相反，频率域中的分布可以通过反傅里叶变换（逆变换）转换回空间域中的分布：

$x_k = \frac{1}{n} \sum_{n=0}^{n-1} X_n e^{\frac{2\pi i}{n} k n}$

反变换的空间域系数 x_k 通常是复数，除非频率域的系数 X_n 满足对称性 X_{n-k} = X_k^*，此时所有 x_k 都是实数。

RooFFTConvPdf 类

RooFFTConvPdf 类实现了以下算法，用于计算类型为 M(x) = T(x) * R(x) 的圆卷积：

​ 1. 将 T(x) 采样到数组 t_i 中，并将 R(x) 采样到数组 r_i 中；

​ 2. 对数组 t_i 和 r_i 进行傅里叶变换，得到 T_i 和 R_i 频率域系数；

​ 3. 在频率域中计算卷积： M_i = T_i \cdot R_i；

​ 4. 对数组 M_i 进行反傅里叶变换，得到 m_i 空间域系数；

​ 5. 通过插值将数组 m_i 表示为连续函数 M(x)。

该方法的大部分计算工作集中在（逆）离散傅里叶变换的计算上。离散傅里叶变换的快速计算是信号处理领域的一个重要研究课题，并且已有很好的算法可以高效地计算这些变换。RooFit 使用了免费提供的 FFTW3 包，它通过 TVirtualFFT 类与 ROOT 进行接口连接，并提供了最快的离散傅里叶变换实现之一。这意味着，要使用 RooFFTConvPdf，你必须确保在 ROOT 安装中包含了 FFTW。

6 构建多维模型

6.1 引言

许多数据分析问题涉及不止一个观测量。当观测量之间的相关性包含大量信息时，从这些分布中提取信息可能会变得复杂。为了解决这样的多变量问题，通常使用两种主要方法。

第一种方法是使用机器学习的多变量分析（MVA）来构造一个一维的判别量（discriminant），尽可能捕获多维分布中包含的信息。这种方法功能强大且易于管理，得益于像 TMVA 这样的工具，它为各种技术（例如神经网络、提升决策树（Boosted Decision Trees）、支持向量机（SVM）等）提供了统一的训练和应用接口。最终的拟合通常在判别量或未用于判别量的一剩余观测量上进行，以提取最终结果。

另一种方法是为所有输入观测量构建一个显式的多维信号和背景描述，形式为多维似然分布。这种方法较少依赖自动化，除非所有观测量都是不相关的，但理论上它的能力不低于 Neyman-Pearson 引理所给出的任何多变量分布的最优判别量：

$D(\vec{x}) = \frac{S(\vec{x})}{B(\vec{x})}$

其中S(x)和B(x)分别是真正的信号和背景分布。当经验分布S(x)和B(x)与真实分布匹配时，可达到上述最优判别量。这种方法的挑战来自两个方面: 需要对预期分布的形状有深入的了解，需要找到一个能够描述该多维分布的显式公式。第一个挑战实际上是这种方法的一个特性：如果处理得当，模型中仅包含您能够很好理解和解释的参数，且仅具有您认为相关的自由度。而机器学习训练的判别量参数可能从完全不可解释（例如神经网络权重）到部分可理解（例如未提升的决策树）不等。

RooFit 在这一过程中扮演的角色是简化第二个挑战，即直观地为具有相关性的多维分布构建显式模型的能力。图 21 所示的二维模型便是 RooFit 功能的一个例子。该分布为：对于每个 $ y $ 值，$ x $ 的分布是一个高斯分布，且高斯分布的均值依赖于 $ y $；同时，$ y $ 的分布本身也是一个高斯分布。

在纯 C++ 中，准确地描述这种分布及其相关性的二维概率密度函数 $ H(x, y) $ 是一项具有挑战性的任务。然而，在 RooFit 中，仅需四行代码即可按照此处描述的方式构建分布：编写一个条件概率密度函数 $ F(x|y) $，表示给定 $ y $ 值时 $ x $ 的分布；构建描述 $ y $ 分布的概率密度函数 $ G(y) $；将这两部分信息组合起来。RooFit 能够表示具有相关性的多维分布的能力来源于其灵活的概率密度函数归一化策略，该策略允许任意概率密度函数用作条件概率密度函数。

在本节的其余部分，我们将指导您以多种方式构建多维模型的基本操作。多维模型中特定的使用问题将在第 7 章讨论。

6.2 使用多维模型

在深入探讨如何最佳构建多维模型之前，我们先简要概述一下RooFit的绘图、拟合和事件生成接口是如何扩展到具有多个观测量的模型的。为了说明所有基本概念，我们构造了一个在观测量x和y上的二维RooGenericPdf。我们选择了最简单的公式，因为多维概率密度函数（p.d.f.）的内部结构与绘图、拟合和生成接口无关：这些接口的工作方式不受模型结构的影响。

RooRealVar x("x","x",-10,10);  
RooRealVar y("y","y",-10,10);  
RooRealVar a("a","a",5);  
RooRealVar b("b","b",2);  
RooGenericPdf f("f","a*x*x+b*y*y-0.3*y*y*y",RooArgSet(x,y,a,b));  

6.2.1 评估

在第2章中已经解释，当评估一个RooFit的概率密度函数时，必须明确指定哪些变量是观测量。如果有多个观测量，只需传递包含所有观测量的RooArgSet，而不是单个RooAbsArg：

f.getVal(RooArgSet(x,y));

6.2.2 生成和拟合

由于生成和拟合过程自然地定义了观测量，因此接口扩展到多个观测量的方式十分直接。在事件生成中，可以传递包含观测量的RooArgSet，而不是单个观测量；在拟合中，由于所传递的RooDataSet已经定义了观测量（在本例中为两个观测量），接口无需任何改变。

// 生成一个二维数据集data(x,y)  
RooDataSet* data = f.generate(RooArgSet(x,y),10000);  
// 将二维模型f(x,y)拟合到数据data(x,y)  
f.fitTo(*data); 

6.2.3 绘图

绘图接口依然保持不变，但现在可以为每个观测量单独生成一个图像：

// 绘制数据data(x,y)和模型f(x,y)的x分布  
RooPlot* framex = x.frame(); 
data->plotOn(framex); 
f.plotOn(framex);  

// 绘制数据data(x,y)和模型f(x,y)的y分布  
RooPlot* framey = y.frame(); 
data->plotOn(framey); 
f.plotOn(framey);  

上述例子的输出如图22所示。图22中的两个图像能直观地符合预期，这并非完全是偶然的，它反映了RooFit在后台为你完成的一些记录工作

绘制数据十分简单：要获得数据data(x,y)的x分布，只需忽略y值，并用x值填充直方图。而绘制概率密度函数（p.d.f.）则稍微复杂一些：需要绘制gaussxy(x,y)在x或y上的投影，以得到与数据相同解释的分布。RooFit默认使用的技术是积分

$ F_x(x;p) = \int p(x, y;p) , dy $

RooPlots的一个关键特性是，它会跟踪需要投影的观测量：如果你在x的RooPlot中绘制一个数据集D(x,y,z)，系统会记住观测量y和z的存在。任何随后在该图框上绘制的具有观测量y和/或z的概率密度函数将自动在这些观测量上进行投影。关于任何投影积分的信息都会以消息的形式告知：

RooAbsReal::plotOn(fxy) plot on x integrates over variables (y)  
RooAbsReal::plotOn(fxy) plot on y integrates over variables (x)

关于多维模型使用可能性的完整概述详见第7章。

6.3 模型构建策

现在我们回到本章的核心问题：多维模型的构建。前面部分所使用的整体多维模型在实际应用中很少有用。大多数多维模型是通过使用组合或乘积技术从低维模型构建而来的，如开篇部分描述的示例所示。我们将在这里简要比较这两种技术，并在后续部分详细探讨其技术细节。

6.3.1 乘积法

乘积法是一种将两个或多个具有不同观测量的概率密度函数（p.d.f.）组合成一个更高维、无相关性的p.d.f.的直接方法：

$C(x, y; a, b) = A(x; a) \cdot B(y; b)$

正交p.d.f.的乘积具有以下吸引人的性质：如果输入p.d.f.是归一化的，那么它们的乘积也是归一化的：

$\int \int C(x, y) , dx y = \int \int A(x) B(y)dxdy= \int A(x) , dx \cdot \int B(y) , dy = 1$

6.3.2 组合法

组合技术通过用至少一个新观测量的函数替换某个参数来构造多维模型。例如，给定一个以观测量 x 为自变量的高斯函数 $\text{Gauss}(x; m, \sigma)$ ，可以通过以下方式创建一个以 x 和 y 为观测量的二维p.d.f. ：

$F(x,y; m,\sigma,a) = \text{gauss}(x, M(y), \sigma)$ 其中 $M(y)=m+a \cdot y$

我们在第4章已经见过这种技术，当时我们用它来调整现有形状的参数化。这里唯一新增的概念在于其解释：并没有什么限制新引入的变量 y 不能作为观测量使用，因此实际上我们将一维高斯p.d.f.扩展为一个基于第二个观测量 y 的均值偏移的二维高斯函数。

组合法的一个重要优势是，它可以简单地引入观测量之间的相关性，这是乘积法无法直接实现的。

6.3.3 组合与乘积的结合

尽管组合法能够生成功能完善的多维p.d.f.并能很好地控制相关性，但通常不能很好地控制新引入的观测量的分布。在上述代码示例中， x 的分布及其如何随 y 变化是明确的，但 y 本身的分布并不清晰。因此，组合法生成的p.d.f.通常用作条件p.d.f. F(x|y) 而不是联合p.d.f. F(x, y) 。随后，再与一个独立的p.d.f. G(y) 相乘，形成一个良好控制的二维模型：$H(x, y) = F(x|y) \cdot G(y)$

这种方法结合了两种技术的优势：组合法用于引入相关性，而乘积法用于生成良好控制的观测量分布。

6.4 通过乘积构造多维模型(Multiplication)

我们通常使用乘积去构建多维函数模型

6.4.1 RooProdPdf类

在RooFit中，任何形式的概率密度函数（p.d.f.）乘积都通过RooProdPdf类构造。以下是一个简单示例：

RooRealVar x("x","x",-10,10); 
RooRealVar meanx("meanx","mean of x",0);  
RooRealVar sigmax("sigmax","sigma of x",2);  
RooGaussian gx("gx","Gaussian for x",x,meanx,sigmax); 

RooRealVar y("y","y",-10,10); 
RooRealVar meany("meany","mean of y",0); 
RooRealVar sigmay("sigmay","sigma of y",2);  
RooGaussian gy("gy","Gaussian for y",y,meany,sigmay);  

RooProdPdf gaussxy("gaussxy","gx*gy",RooArgSet(gx,gy));

在这个例子中，我们通过RooProdPdf将两个一维高斯p.d.f. gx 和 gy 相乘，构造了一个二维p.d.f. gaussxy 。这种乘积p.d.f.可以像z之前的整体p.d.f. f 一样用于拟合和生成。

RooDataSet* data = gaussxy.generate(RooArgSet(x,y),10000) ;
gaussxy.fitTo(*data) ;

RooPlot* framex = x.frame() ;
data->plotOn(framex) ;
gaussxy.plotOn(framex) ;

RooPlot* framey = y.frame() ;
data->plotOn(framey) ;
gaussxy.plotOn(framey) ;

RooProdPdf类能够将任意数量的组件相乘。在此示例中，我们将两个一维p.d.f.相乘，但同样可以组合例如7个一维p.d.f.或2个五维p.d.f.。

6.4.2 内部实现

尽管拟合、绘图和事件生成接口与整体p.d.f.的接口看起来相同，但对无相关性p.d.f.的乘积操作，其背后的实现与整体模型存在显著差异。首先，对于正交p.d.f.的乘积，不需要显式计算归一化，因为它们通过构造自然归一化：

$\int \int C(x, y) , dx y = \int \int A(x) B(y)dxdy= \int A(x) , dx \cdot \int B(y) , dy = 1$

在绘图中，投影积分可以按照类似的方法简化

$\int C(x, y) , dy=\int A(x) B(y)dy = A(x) \cdot \int B(y) , dy = A(x)$

这种简化是通过对输入的RooProdPdf结构进行逻辑推导，而不是通过强制计算实现的。

事件生成同样利用了因子化的性质。在 C(x, y) 的示例中， x 和 y 的分布可以分别从 A(x) 和 B(y) 独立采样，然后再将结果组合，而不需要对联合分布直接采样。这种方法不仅减少了问题的维度，还允许将观测量的生成委托给组件p.d.f.，而这些组件可能实现了一种比默认的接受/拒绝采样更高效的内部生成器。如图24所示，该分布生成过程充分体现了这种优化的优点：通过分解联合分布，可以高效生成所需的多维数据集。